Caveat: Unless you have participated in this simulation, parts of this are going to read weird. It’s ok, you can skip them; get right to the method.
Network theory measures, and in particular Burt’s theory of constraints, were applied to the goals of an eleven party negotiation simulating major groups with concerns for the future of Afghanistan, and compared with the actual outcomes of the negotiations. One group showed remarkable performance despite having low negotiating leverage, suggesting a possibility of exploiting information asymmetries. This paper examines alternative possibilities for the outcome, and raises the possibility that if this case is representative, mapping and measuring the network of goals could have predictive power over outcomes in multiparty negotiations.
Introduction
On Saturday, November 1st, 2008, I participated in a multiparty negotiation simulation as part of the New York University Global Affairs class: “Building Democracies: Case Study Afghanistan.” The simulation had one surprising result: the small team of NGOs received an inordinate share of negotiation attention relative to what they could provide in comparison to the other participants.
The possible reasons we are explore are purely structural. We explicitly ignore variance in skill and experience in negotiations of the participants. While these clearly could have influenced the outcomes, we had neither ability to measure nor control for these variances.
Looking for structural reasons why this may have come to pass, we explore the possibility of arbitrage through information asymmetries. In order to test for this possibility, we look at the characteristics of the negotiations to see whether the NGOs have both opportunity to discover and opportunity to exploit any discovered asymmetries. To rule out other structural reasons for the success of the NGOs, we compare the results to two other groups across three other measures. The two groups are those representing the U.S. Military and representing the President of Afghanistan. The three measures including negotiation power as expressed by strength of of the group’s best alternative to no agreement (BATNA)[FU1981]; common desire to negotiate between groups that want something from each other; and whether there was an opportunity cost in having goals spread across too many other teams.
Overall, we find that BATNA or information asymmetries explain well the success of the U.S. Military throughout the simulation; the President of Afghanistan was in a good position to discover, but not act upon, information asymmetries; and the NGOs success is, of the measures compared, best explained by information asymmetries.
Background on the Simulation
NOTE: The simulation was designed by Patrica DeGennaro, Adjunct Professor of the Global Affairs department at New York University. Out of courtesy, full details of the simulation are withheld and included is only a rough description of the details pertinent to the analysis. Requests for more details will be fulfilled at her discretion, and should be directed to Professor DeGennaro by email to [pd51 at nyu.edu].
The simulation comprised of eleven groups with individual goals and constraints provided explicitly on a group by group basis. A twelfth passive role, the Grand Mullah, is included. One of the eleven roles assumed did not participate in the simulation and was not included in the analysis.
The goals of each group were designed to be as realistic as possible given the limitations of classroom execution, and required each role to negotiate with at least two other groups.
The three main roles the majority of our discussion will cover are: the U.S. Military, the President of Afghanistan, and two non-governmental organizations – human rights and humanitarian aide. The two NGOs largely worked as a bloc, and will often be referred to collectively as the NGOs. For the curious, a full list of the roles can be found in the Methods and Results section of Network Constraint.
Traditional Game Theory Measures
There is extensive literature on the application of game theory to negotiations, including [Strauss1978] and [Brams2003]. This paper assumes a basic level of knowledge about game theory, and information incomplete and one-time games in particular.
Opportunities to Negotiate
The first measure we examine is whether mutual desire to negotiate played a part in the general success or lack-there-of of our three groups in question. We use the number of other teams each has where both want something from each other. Since each goal required negotiation with another party, thus count intuitively represents the amount of opportunity each team has to accomplish a goal. The results, however were surprising.
The President of Afghanistan, of all of the teams, had the highest number of opportunities to bargain to solution. Comparatively, both the NGOs and the US Military had low to average alignment by this measure, but neither had the lowest. Those with the lowest did not perform to either extreme during the simulation. All things equal, the results here are counter-intuitive and would be an interesting topic for future research.
Look to determine whether there was a distraction cost associated with negotiating with a large number of groups, We looked at the number parties:
- each wanted to negotiate with
- that wanted to negotiate with each party
- where those wants overlapped
Under none of those scenarios did the U.S. Military and the NGOs resemble each other; nor show strong contrasting results with the President of Afghanistan. The cost of negotiation alone is insufficient to explain the differences.
Each groups’ Best Alternative To No Agreement (BATNA), or fall-back position should a negotiation fall through, is a common measure of how hard a group will be willing to push for their own goals, and is a strong indicator of the expected outcomes.
The U.S. Military, with strong funding and one of the few groups with the ability to move around the country with safety, clearly has a strong BATNA.
The NGOs, by contrast, are small and have little to offer except their goals. Incapable of even achieving those without external security, they have very poor BATNAs.
The President of Afghanistan, arguably, has a low BATNA. His office is one of clear influence, but largely reliant of others to enforce its authority.
BATNA could explain the success of the U.S. Military and the relative inattention the President of Afghanistan received, but does not explain the success of the NGOs. Clearly, BATNA is not the only factor in play.
Network Effects
Until now, we have been using relatively common measures which require little explanation. Introducing the new measure of network effects, we will provide an introduction to the theory, the process, and finally an analysis of the outcomes.
Information Asymmetries
Information asymmetries consist of an advantage when one or more, but not all, parties in a negotiation have better information than the other parties [Akerlof1970]. The situation often involves a buyer better informed than a seller as in the case of insurance companies knowing more about risks in health care than the covered patients[Arrow1963], but the reverse is equally applicable. There are two requirements for an information asymmetry to be relevant: the opportunity to discover and the opportunity to act. It is not enough to simply possess the information, one must be able act on the information. The NGOs had both, whereas the President of Afghanistan had good opportunity to discover, but little opportunity to act. This will be discussed further in the analysis section.
First we create a directed network graph of goals to express the potential relationships between the groups. For example, if A and B each want something from each other, and B wants something from C, but C wants nothing from B; we have a network that looks like:
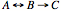
We create this network across all 11 groups included in the scenario; including the Grand Mullah, but excluding the village elder. The village elder was excluded as she did not participate in the simulation. The Grand Mullah participated in the simulation, but passively, and therefore did not have a significant impact on the construction of the network despite unknown goals.
I was not able to glean much information from the graph of relationships in this simulation, but that is not always the case. The graph information must be collected to calculate the constraints, so it is worthwhile to graph them anyway.
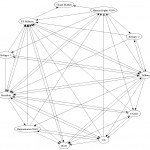
Figure 2 sets up all nodes around a circle. Treating each node identically, this method is good for identifying nodes with many, or few, inputs and outputs relative to the others. Here we see the large number of inputs (wants from) the U.S. Military and the President of the Afghanistan; and the lack of any outputs (wants of) the Grand Mullah.
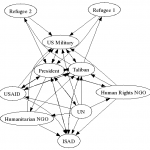
Figure 3 shows the same network represented through a “spring model” after [FR1991]. This method of display begins to show how all of the relationships pull on the nodes in concert. Nodes toward the center of the graph tend to be more critical (central) to and have opportunity to influence the flow of goods, services, and information throughout the network.
By design, all of our relationships are treated equally. This simplification is not a requirement of the modeling, but instead because we do not have enough information to judge the relative strengths of the wants and needs of each team. If more was known, then each relationship can be assigned a numerical value indicating the strength of the goal relative to all others of the same node; they need not measured relative to the goals of any other group. This relative scaling is of strong assistance during measurement, as the lack of need for consistent scaling allows valuation of relationships by each group in question and without coordination.
For our use, with goal desires unknown on a relative comparison, we will assume all goals are identically valued, and use the value of 1.
Burt introduced a method of describing and calculating how constrained a node is by its neighbors [Burt1992]. This constraint measures how much control over the flow through the network to a node its neighbors have. If a node has a low constraint, it has independent paths to the network. If the node has a high constraint, it shares paths with many of its neighbors.
To understand network constraint, consider the ability of nodes A and B in the following figure. Consider their relative abilities to control the flow of information to their neighbors.
i,j,k
Distinct nodes in a network.
Vij
The value of the relationship from node i to node j. If the relationship does not exist, Vij = 0. For the purposes of our analysis Vij ≥ 0, Vii = 0.
Pij = Vij/Sum(Vik|i≠k) (1)
Algorithm 1 provides the proportion of the total value of the all relationships from node i that Pij represents.
Cij = (Pij + Sum(Pik * Pkj|k≠i,j))^2 (2)
Algorithm 2 provides us with our first step in constraint; the constraint imposed on a node by one of its neighbors, j.
Ci = Sum(Cij|j≠i) (3)
Algorithm 3 shows the total constraint of node i.
Using the Burt constraint methodology described above on the previously created network graphs, constraints were calculated for each group, and then normalized so that 1 was the maximum constraint. This is not part of the Burt methodology, added here to more easily compare to other networks in the future. Each of the teams, presented by order presented in the simulation, were ranked from least to most constrained for ease of convenience based on their Burt constraint score. Teams with identical constraint score were provided the same rankings.
| Team | Constraint | Ranking |
|---|---|---|
| U.S. Military | 0.57 | 1 |
| NGO – Human Rights | 0.58 | 2 |
| President of Afghanistan | 0.62 | 3 |
| Taliban | 0.62 | 3 |
| NGO – Humanitarian | 0.68 | 4 |
| USAID | 0.68 | 4 |
| UN | 0.69 | 5 |
| ISAD | 0.71 | 6 |
| Refugee 1 | 0.72 | 7 |
| Refugee 2 | 0.72 | 7 |
| Grand Mullah | 1 | 8 |
From the expression of the group constraints contrasted with our other measures (BATNA, alignment, and opportunity costs); network constraint is the first measure which correctly ranks the observed outcomes of the simulation for the U.S. Military, the NGOs, and the President of the Afghanistan. The ranking of the President of Afghanistan seems high relative to the outcome of some of the other groups listed, but this is not entirely surprising.We know for information asymmetries to be factor, an entity must be in a position to both discover the asymmetries as well as act upon them. In our simulation, all of the groups were mobile – free to move about the space and speak with any group at any time – except the group representing the President of Afghanistan. This group was explicitly excluded from moving about; thereby eliminating any opportunity to act on information asymmetries discovered unless the right parties happened to return to carry on further discussions. Network constraint and information asymmetry predicts that if the mobility limitation were eliminated, the group portraying the President of Afghanistan would have a significantly better opportunity to reach the goals placed upon the group by the simulation.
Conclusions and Suggestions for Further Research
Of the measures examined – information asymmetries via network constraint, BATNA, negotiation opportunity alignment, and opportunity costs – information asymmetries was the best single predictor of the observed results. Combined with BATNA, this appears promising in creating predictors to observed outcomes from structural factors in multiparty negotiations.
Negotiations are complex situations to organize, and results are dependant upon a large range of variables; many of which are difficult to identify and measure; so it is no surprise that the results of this simulation seem best described by a number of factors.
Examining goal alignment produced counter-intuitive results, with the most opportunities to negotiate resulting in poorer goals.
The opportunity cost of negotiating seemed measured as the number of other teams looking to negotiation with (incoming relationships), the number of teams each wanted to negotiate with (outgoing relationships), as well as the number of common partners (is this a repeat w/ goal alignment?) all showed unremarkable differences between the groups in question.
BATNA seems to offer a strong representation for both the U.S. Military and the President of Afghanistan. It did not show much value in predicting the unsuspected outcomes with NGOs.
Network analysis was the only method to identify the NGOs as high level groups. Taking into account that the NGOs ended up working together, they could have taken advantage of the low constraint of the Human Rights NGO.
Network analysis seems insufficient to explain everything, however, it is the only method to correctly place both the U.S. Military and the Human Rights NGO before the President of Afghanistan.
Over all, the premise is promising and requires extensive further analysis through more simulations, and expanded ranking about ability to get goals accomplished or others measure of power
Fruchterman and Reingold. Software-Practice & Experience 21(11), 1991, pp. 1129-1164.
Thank you for the informative article.
I have utilized network analysis as both a negotiation training and evaluation tool as part of research into the use of network training as an accelerator of collaborative enterprise. I would be interested to learn how widespread network analysis is being used within negotiation research, teaching and practice. I noted the absence of network analysis in the article references so would be interested to know of any links to the negotiation literature.