Exploring Novelty Through Entropy: A Journey in Behavioral Diversity
What if we could measure surprise itself? Not the subjective experience of it, but its mathematical essence, distilled into equations that guide us toward the genuinely unexpected? This question led me down a rabbit hole where information theory meets evolutionary computation, where the mathematics of uncertainty becomes a compass for discovering behavioral diversity.
The Paradox of Searching for the Unknown
Consider the fundamental paradox of novelty search: how do you find what you don’t know you’re looking for? Traditional optimization assumes a destination, a fitness peak to climb. But what happens when the landscape itself is the goal? When every peak discovered reveals new valleys, and every valley opens onto unexplored plains?
Entropy enters this story like a character from another narrative entirely. Borrowed from thermodynamics and information theory, it measures disorder, uncertainty, the number of possible states a system might occupy. Yet in our context, entropy becomes something more poetic: a measure of behavioral richness, a quantification of the very quality that makes something interesting.
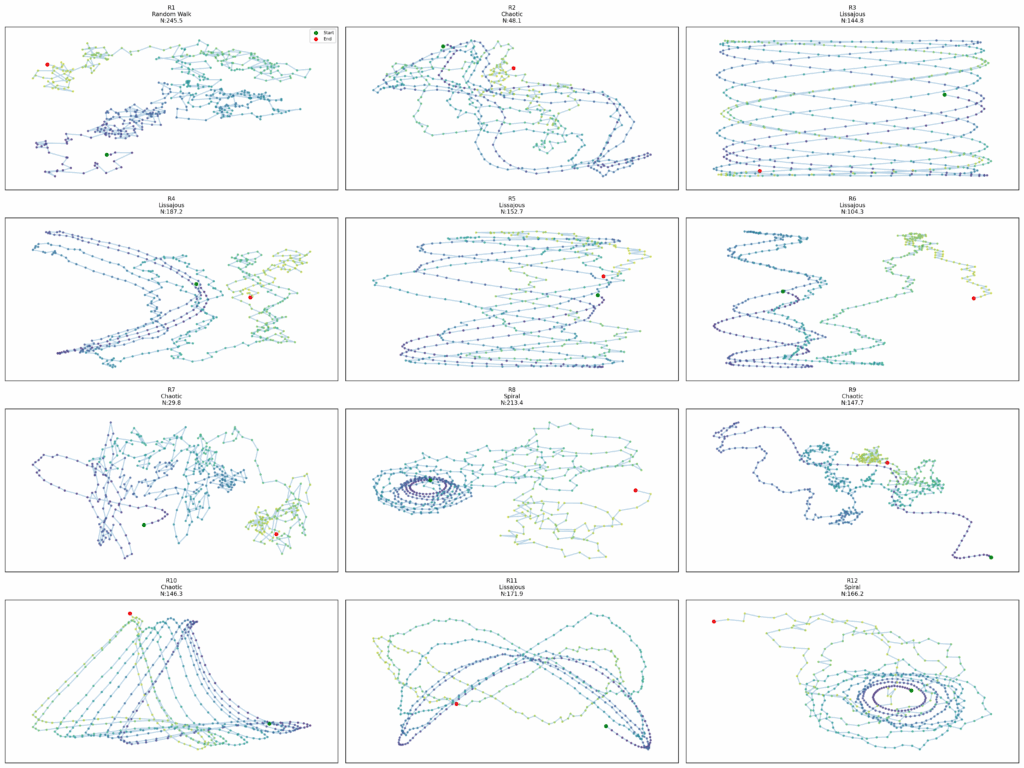
The trajectories traced by our artificial agents tell stories that no human author could have conceived. Some spiral outward like galaxies being born, others oscillate with the rhythm of unknown songs, and still others chart chaotic paths that never quite repeat, like Borges’s labyrinth that changes each time you walk it. Each pattern emerges not from deliberate design but from the interplay between simple rules and the relentless pressure to be different.
Information as the Currency of Creativity
In this framework, information becomes the currency of creativity. Every behavior carries an information signature, a pattern of spatial coverage, directional choices, and velocity variations that can be decomposed into probability distributions. The entropy of these distributions tells us something profound: how surprised we should be by what we’re seeing.
But here’s where it gets interesting. The system doesn’t just measure absolute entropy. It measures relative entropy, asking not “how complex is this?” but “how does this complexity differ from its neighbors?” This shift transforms entropy from a static measure into a dynamic force, creating gradients of novelty that pull the population toward unexplored territories.
The mathematics reveal something unexpected: novelty has a topology. Behaviors cluster and spread across an abstract landscape where distance is measured not in space or time but in surprise. The system navigates this landscape like an explorer without a map, using only a compass that points toward the unexpected.
The Ecology of Difference
What emerges from this process resembles nothing so much as an ecology. Not an ecology of living things competing for resources, but an ecology of patterns competing for uniqueness. The distribution charts reveal a startling truth: diversity maintains itself. No single behavioral strategy dominates because dominance itself would reduce the novelty that the system rewards.
This self-organizing diversity suggests something profound about the nature of creative spaces. Perhaps all creative endeavors naturally evolve toward this kind of ecological balance, where different approaches occupy different niches not because they’re optimal for some external task, but because they’re optimal for being themselves.
The speed profiles of different behaviors read like musical scores, each encoding a different rhythm of movement through space. Some maintain metronomic regularity, others build to crescendos and fade to silence, and still others improvise jazz-like variations that never repeat. Together, they form an orchestra where every instrument plays a different song, yet somehow the cacophony resolves into something greater than noise.
Diminishing Returns as a Feature of Discovery
The improvement curves tell a story as old as exploration itself. Early generations discover behavioral continents: broad patterns like spirals, oscillations, and random walks. Middle generations map the coastlines, finding variations and hybrid forms. Later generations must venture inland, discovering the subtle variations that distinguish one chaotic attractor from another.
This pattern of diminishing returns isn’t a flaw in the system; it’s a fundamental feature of any genuine exploration. It tells us that we’re not just generating random variations but actually mapping a space of possibilities. Each discovery makes the next one harder to find, not because we’re running out of ideas, but because we’re raising our standards for what counts as truly novel.
The system’s response to these plateaus reveals a kind of meta-creativity. When simple mutations no longer yield surprises, it increases mutation rates. When local search exhausts nearby possibilities, it encourages larger jumps through behavioral space. The search process itself evolves, becoming more sophisticated as the easy discoveries are exhausted.
The Philosophy of Measured Surprise
Using entropy to guide novelty search illuminates something fundamental about the relationship between information and creativity. We often think of creativity as ineffable, beyond measurement. Yet here we see that at least one aspect of it, the generation of novel patterns, can be captured mathematically.
This doesn’t diminish the mystery of creativity; it deepens it. The fact that we can measure novelty doesn’t tell us why we value it, why humans and now our algorithms seek it out with such persistence. Perhaps the drive toward novelty is written into the mathematics of information itself, a fundamental force like gravity or electromagnetism, pulling systems toward greater complexity and diversity.
The visualizations offer windows into this abstract space. Each trajectory is a meditation on difference, a solution to the problem of being unique in a world of other unique things. Some achieve uniqueness through simplicity, tracing clean geometric forms. Others embrace complexity, weaving patterns that challenge our ability to categorize or predict.
Emergence and the Architecture of Surprise
What strikes me most profoundly is how surprise itself has an architecture. The system doesn’t just generate random behaviors and select the weird ones. It constructs a framework where surprise can emerge systematically, where the pressure to be different creates its own logic and beauty.
This architecture reveals itself in the phase transitions of the search process. Early on, any deviation from the norm counts as novel. But as the population diversifies, novelty requires increasingly sophisticated innovations. The system must discover not just new behaviors but new categories of behavior, new ways of being different.
The interplay between local and global diversity creates a kind of creative tension. Local diversity ensures that neighbors in the population explore different variations, while global diversity ensures that the population as a whole covers different regions of possibility space. This dual pressure creates a dynamic equilibrium where innovation happens at multiple scales simultaneously.
Questions at the Edge of Understanding
This exploration raises questions that stretch beyond the boundaries of our current understanding. If entropy can guide us toward novelty in behavioral space, what other spaces might we explore with similar principles? Could we use entropy to discover novel molecular structures, musical compositions, or philosophical arguments?
The relationship between constraint and creativity also deserves deeper consideration. Our system operates within constraints: bounded space, limited parameters, finite computational resources. Yet within these constraints, it discovers seemingly infinite variety. Perhaps constraint isn’t the enemy of creativity but its necessary partner, providing the resistance against which novelty can define itself.
I find myself wondering about the nature of the space we’re exploring. Is it truly infinite, or does it have boundaries we haven’t yet discovered? Are there fundamental limits to behavioral diversity, or does every discovery open new dimensions of possibility?
The Infinite Game of Difference
As I reflect on this journey through entropy-driven novelty search, I’m struck by how it mirrors larger patterns in nature and culture. Evolution itself might be seen as a massive novelty search, using environmental niches as a kind of entropy measure. Human culture, too, seems driven by a similar dynamic, constantly generating new art, ideas, and ways of being.
The diminishing returns we observe might not be a limitation but a feature that drives ever-greater creativity. As the obvious innovations are exhausted, we’re forced to become more clever, more subtle, more sophisticated in our search for the new. The difficulty itself becomes a kind of selection pressure, favoring not just novel behaviors but novel ways of generating novelty.
Perhaps this is why I find this approach so compelling. It suggests that the search for novelty isn’t just a computational problem but a fundamental aspect of complex systems. By understanding how to measure and guide this search, we’re not just building better algorithms; we’re gaining insight into the nature of creativity itself.
The journey continues, each experiment revealing new questions, each answer pointing toward unexplored territories. In that sense, novelty search is its own best example: an endless exploration that generates surprise not just in its outcomes but in what it teaches us about the very nature of exploration.