metrics

Network Analysis Application to Game Theory (with Software)

April 4, 2009 erichLeave a comment

When will network analysis provide additional insight into game theory? In a word: inequality.

There must be some form of quantifiable inequality in the game: access, strength of relationships, goals, etc. This difference creates opportunities for the individual players to use information (or resource) asymmetries and broker to their benefit.

On the left all of the arrows representing the relationships have the same weight, representing the same value, in both directions and between all nodes. On the right, the arrows have different weights between nodes. The greater the inequality, the more effective the application of network analysis.

The relationships depicted could be import/export pairs ($ or volume), contract frequency, or even strength of social relationships. Do not underestimate the potential utility in measuring based on qualitative values, such as strength of relationships. Using them can not only be quite effective, but they can often be much easier to calculate than one might suspect at the onset. Here’s why.

The analysis method I suggest looks at all of the weights relative to the originating node. It does not matter whether you can accurately value A’s relationship to B versus B’s relationship to A, as long as you can compare A’s relationship to B versus A’s relationship to C. From the point of data collection, even an intuitive estimation these comparative values will provide insight. Thus knowing A wants something from B more than A wants the alternative from C, is often sufficient.

Looking at the perspective of access, this is represented in the shape of the network as “holes” or gaps. There are technical definitions, but it’s usually quicker to understand through an image. Compare:

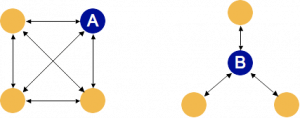From the perspective of the two darker nodes A and B, they clearly have different opportunities to act as brokers based on the holes (or lack thereof) in the network.

Using the two of these together has shown some promising results.

Here is a simplified version of one of the tools I wrote to calculate the opportunity to act as broker based on the value of relationships and the network. The TAR file contains the simplified program written in Perl, and two sample CSV network files: one similar to each network in the second image. The program relies on a module not yet indexed by CPAN, but is available there.

The calculation is called the network constraint, after Ronald Burt’s work. The lower the constraint, the larger the opportunity to act as a broker, i.e. perform well in the game based on network structure.

I am in the process of requesting CPAN to host the Perl module, in registered space, so stay tuned.

[for an older version of the code, with some egregious bugs, but all in one place and no extra downloading, get it here]

/Message: Authority Is A Highly Charged Particle

December 31, 2008 erichLeave a comment

I’ve discussed my thoughts on authority before and I think follower count is a poor measure; but Stowe Boyd as has a great post (where the name for this post came from) summing up much of the controversy.

Two things I particularly like about the post: his spelling out why follower count is not without merit as a measure, and his unshy conviction that influence is a good thing.

To these I’ll add one short thought and one quote. Follower count, for all of its failings is the single measure we can all agree on. That alone is powerful. As for influence:

It is the pressure of our peers, after all, that gives us the support to try things we otherwise wouldn’t have. — BILL TREASURER, Right Risk

A very happy, healthy, and prosperous New Year to you and your social network. Keep connecting.

Predict Attention in Social Networks

August 2, 2008 erichLeave a comment

People distribute attention according to a power-law distribution.

Power-laws have long been associated with distribution of quantity of links individuals in social networks have. My on-going research suggests that power-laws not only describe distributions at the network level, they also describe distribution at the individual level. We communicate in a power-law distribution with our contacts, by frequency. Initial analysis also suggests we spend time communicating with each other according to a power-law.

The distribution analysis for frequency was conducted across six social networks of various types ranging in size from fewer than 100, to more than 6,000 individuals. Most SN research has been conducted on smaller networks (fewer than 100 individuals); so testing across a wide range of sizes both confirms earlier results and suggests that size is not a factor in the power-law distribution. I was concerned about possible distortion on small networks due to implications from Dunbar’s Number. It turns out that small networks are indeed different, which I am not going to go into here, but they still fit these distributions.

Analysis on any complete sub-set, will still fit these pattern. By complete, I mean that connections between any two individuals in the sub-set, must be the same as in the whole set. The value is the introduction of the ability to sample, and to operate over a network recursively. Similarly, much information can be gained about a larger network, even if the data you have is incomplete.

This distribution may allow us to accurately predict impact of changes to any social network. By measuring the current state, we can estimate the impact of adding/removing people and connections. This could be of tremendous value pursuing in any social goal creating by facilitating cohesion, culture, and the like.

I intend on publishing the results and methodology. If you are looking for that level of detail you’ll have to wait, but mail me (erich at howweknowus.com) if you would like to discuss.