Daring Fireball: Open and Shut

erichLeave a comment

John Graber of Daring Fireball has a great (albeit occasionally snarky) post challenging the value of “open” for shareholder value in technology companies.

The key point he starts to discuss, and then backs away from, is the value of externalities contributing to create better products faster.

Tim Wu also hints at this in his piece in the Newyorker, which kicked off Graber’s conversation. I’d like to hear more from both on this.

With an increasing demand for technology solutions to increasingly complex and evolving business problems, there’s a lot of money for whomever solves them. Share the wealth, and I bet we’ll provide our customers value faster now, and as the problems continue to change.

Life in a Networked Age

erichLeave a comment

John Robb, who brought us the term “open source warfare,” wallops the concerns of governance of our increasingly global network:

A global network is too large and complex for a bureaucracy to manage.  It would be too slow, expensive, and inefficient to be of value.  Further, even if one could be built, it would be impossible to apply market dyanmics [sic] (via democratic elections) to selecting the leaders of that bureaucracy.  The diversity in the views of the 7 billion of us on this planet are too vast.

http://globalguerrillas.typepad.com/globalguerrillas/2013/02/life-in-a-networked-age-.html

Transnational Corporation Networks Affect the Market and Stability

erichLeave a comment

The structure of the control network of transnational corporations affects global market competition and financial stability. So far, only small national samples were studied and there was no appropriate methodology to assess control globally. We present the first investigation of the architecture of the international ownership network, along with the computation of the control held by each global player. We find that transnational corporations form a giant bow-tie structure and that a large portion of control flows to a small tightly-knit core of financial institutions. This core can be seen as an economic “super-entity” that raises new important issues both for researchers and policy makers.

http://www.plosone.org/article/info:doi/10.1371/journal.pone.0025995

3 Recommendations on Process Scale Reading

erichLeave a comment

There’s a difference between engineers in most IT shops and in manufacturing.  In IT, there’s a heavier emphasis on design (servers, apps, architectures, etc) than “figuring out how to make things in the greatest numbers and the fastest possible time” [Freedom’s Forge].  With economics what they are today, and the potential operational impact of the industry wide push to cloud, this experience sounds critical.

Let’s build it.

Here’s what I’m starting with.  What are you reading?

Freedom’s Forge by Arthur Herman, recommended by Gunnar – history of the industrialization of the US leading through WWII.  I’m looking for similarities in manufacturing and industry mobilization with hopes of applications to cloud technologies and IT operating models.

The Goal by Eli Goldratt; rereading one of the worst novels ever written.  Genius however, for walking through tools, ideas, and philosophy for improving manufacturing effectiveness.

Pharmaceutical Process Scale-Up by Michael Levin; from the preface: “the procedures of transferring the results of R&D obtained on laboratory scale to the pilot plant and finally to production scale.”

Anything But Random: 1,500,000 Blogs

erichLeave a comment
7,100,000 Relationships Across 1,500,000 blogs

Before Google’s Social Graph API closed last month, I was able to gain access to a reasonable subset: 7,100,000 relationships across 1,500,000 sites (shown below). To be honest, it wasn’t what I was expecting.

The attach rate $latex \left(P\left(k\right) \sim{} k^{-\gamma}\right)$ is pretty close to what Barabasi, Albert, and Jeong found in Scale-free characteristics of random networks. $latex \gamma \sim{} 2.11$ across all, with $latex R^2 = 0.86$. $latex \gamma \sim{} 2.73$ for nodes with fewer than 101 attachments; $latex R^2 = 0.97$.

all nodes
nodes with 100 or fewer edges

Even though that was not much different, what clearly stood out was the sizable amount of neighborhoods. Continue reading “Anything But Random: 1,500,000 Blogs” →

Maximizing Cliques

erichLeave a comment

Finding largest cliques (completely connected sub-graph components) is hard. The best algorithms have run times proportional to 3^(#nodes/3). Triple the nodes = nine times the run length. So what’s a guy without a supercomputer to do but start looking for shortcuts?

Shortcut 1: Maximize for your goals

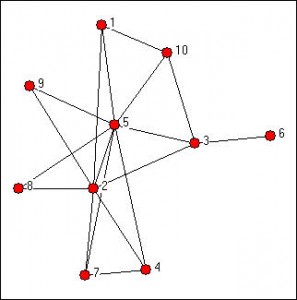
My interest is in characterizing a network, in part, through largest clique size. Since the interest is in size, not quantity, I can start looking for cliques of size N+1 as soon as I find one of size N.

Shortcut 2: Estimate

I’m interested in specific types of networks, social networks. And we can tune for that through size estimation.

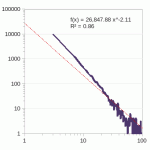
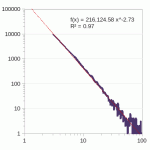
The networks I’ve run through my clique analysis are public (mailing lists, twitter feeds, etc) and generally demonstrate maximum clique size relative to number of active participants and independent of the time observed. I’ve looked at networks sampled for a week to complete observations of 10+ years of conversations.

I have only found once case where the maximum clique size was smaller than ln(# nodes)/2 for these directed networks. When artificially forcing them to undirected networks, the maximum clique size is around double.

Shortcut 3: Cleanse the Data

Now that I have estimated size, every node with fewer edges can be ignored. With that amounting to around (1-1/n)%, for n less than the estimated size, we can cut down the search space.

Shortcut 4: Order your Data

With looking for the largest clique, the more links a node has, the more likely it’s a member of that clique.  So, when you are selecting which nodes to start with, start with the ones with most links.  The sooner you locate larger cliques, the sooner you can stop looking for smaller ones.

Results

Here’s where the “laptop test” comes in: using just a subset of the above, I was able to locate 9-member cliques in an undirected 2,000-node 5,500-edge network in under 5 seconds.  By comparison, on the same machine, it took 5 minutes to locate them using the igraph library in R.

R’s igraph, sadly, ignores edge direction in locating cliques.  But, a run of the above using my code with edge direction completed in about 0.5 seconds.

As an example for larger graphs, I located 15-member cliques in an undirected 75,000-node 220,000-edge network in 20 hours.  R topped out in memory before reaching this size network, and was unable to complete.

Update: It’s been pointed out to me that this has scaled pretty close to n^3.