Are there lower limits to the size of Social Networks worth analyzing? The upper limit seems to be a function of how much time (and compute power) you have, but the lower?
When we do analyses, these are certain characteristics we look for as verification that our models hold. A key characteristic is the shape of the distribution of the number of relationships.
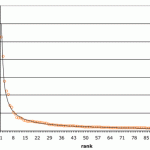
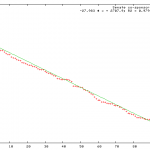
Power-law relationships in social networks are so pervasive, we are surprised when we do not see them. The co-sponsorship of Senate Resolutions, is one such example where we do not see a power-law distribution. In the current session, the 110th, the distribution is just about as different as you can get from a power-law: the result is linear (R-sq > 0.97). My hypothesis is the number of Senators is just too few for the power-law distribution to emerge.
Since there are some significant constitutional barriers to increasing the number of Senators and taking a new sample, in order to test this hypothesis, I opted for locating a different larger set. Wanting to find a network with similar culture and behaviors to control where possible for other variables, I analyzed the House Resolutions from the same period.
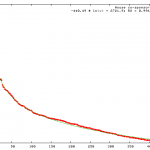
Running the same test across the House Resolutions (1,986 resolutions vs 784 in the Senate), the shape was still not best fit to a power-law. Instead, a logarithmic fit was near perfect (>0.99 R-sq). So, while his does not prove my hypothesis, the shape of a log fit is similar to, but less dramatic than, power-law. This result certainly suggests further exploration.
One possible logical conclusion is distribution forms change with scale. Much of the research on social networks has been on large scale networks, where the math is at its most difficult. At this smaller end of spectrum, especially with the Senate, the networks may be small enough that other analyses could be simpler.
Anthropologist Robin Dunbar, has done research showing humans can keep the interrelations of about 150 people in their heads. More than that number, and we are out of luck. With this in mind, it would make sense that relationship/contact distribution would stretch and distort as the number increases in scale.
So, if you are looking for the key members of a network smaller than “Dunbar’s Number,” there is an easier way to find out who they are: ask. If you can get a few people who are already invested in the network to answer you truthfully, they will be able to give you a really good idea who the key people are.